projet 1 matlab

Faculté des

Sciences

Appliquées

Mécanique Rationnelle

2e candidature 2005-2006

SOLUTION 1 - MATLAB

Version 0.0 du 19 juin 2006

Attention, n’oubliez pas de visualiser l’animation ci-après

Un satellite haltère composé de deux masses ponctuelles de masse inconnue aux extrémités d’un filin de 100 km est en orbite circulaire autour de la Terre à 200 km d’altitude.

L’haltère est perpendiculaire au plan de l’orbite

L’opérateur au sol applique les consignes de manœuvre suivantes qu’il lit dans ses procédures :

- Lorsque le satellite est à son périgée (point le moins éloigné de la Terre), il rétracte le filin pour que les deux masses ponctuelles soient l’une contre l’autre. On simplifiera en considérant que les deux masses ponctuelles sont confondues.

- Lorsque le satellite est à son apogée, il étend de nouveau le filin pour que les deux masses ponctuelles soient à nouveau éloignées l’une de l’autre de 100 km

NOTE : au départ, une idée farfelue d’un mécanicien céleste russe, ce type de phénomène fait l’objet d’étude de la NASA pour voir si on ne peut pas l’utiliser pour des programmes d’exploration du système solaire via des sondes à très faible coût

On demande :

- L’haltère restera-t-elle perpendiculaire au plan de l’orbite

- L’effet de ce mouvement d’extension/rétraction du filin sur l’orbite du satellite.

- Au bout de combien de temps, l’effet sur l’orbite est non réversible. Le phénomène observé est-il réaliste ou exploitable. Si la réponse est non, imaginez d’autres scénarios pour le rendre réaliste et exploitable. On peut jouer sur la longueur du filin jusqu’à des valeurs très grandes pour mieux comprendre.

- Comment pourrait-on selon vous exploiter cet effet dans l’exploration des planètes proches mais quel est l’élément contraignant

- Quelle est l’influence de l’orbite initiale sur la manifestation de cet effet (influence de l’altitude et de l’excentricité de l’orbite)

ATTENTION : CECI N’EST PAS UN RAPPORT DE PROJET AU SENS OU ON L’ATTEND DE L’ETUDIANT. IL S’AGIT DE NOTES DE CORRECTION ECRITES PAR L’ASSISTANT QUI A CONCU LE PROJET. ELLES SONT UTILISES ET POUR GUIDER L’ETUDIANT PENDANT SON PROJET ET POUR SERVIR DE CANEVAS DE CORRECTION UNE FOIS LE PROJET REMIS.

- L’haltère restera-t-elle perpendiculaire au plan de l’orbite

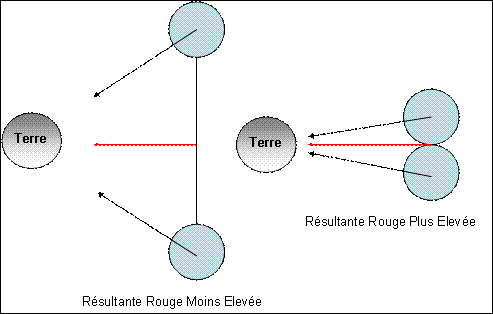
Oui. La Figure 1 montre les forces qui agissent ; les vecteurs noirs sont les forces d’attraction agissant sur les deux sphères séparées. En rouge, c’est la résultante suivant le plan de l’orbite suivant le plan de l’orbite. Dans la direction perpendiculaire au plan de l’orbite, la résultante des forces est nulle. Il n’y a donc aucune raison que le satellite haltère quitte le plan de l’orbite.

- L’effet de ce mouvement d’extension/rétraction du filin sur l’orbite du satellite.

En fait tout repose sur le fait que l’attraction terrestre n’est pas constante ou si on préfère, sur le fait que le champ de la pesanteur varie en fonction de l’altitude ; si les deux extrémités d’un satellite haltère sont liées par un filin très long, ces deux extrémités ne sont pas soumises à la même attraction qu’un point massique de même masse que le satellite haltère situé au centre de masse de ce dernier.

La Figure 1 illustre le phénomène. On maximise l’effet de fronde gravitationnelle.

Donc l’excentricité de l’orbite va croître. On peut se demander d’où vient l’énergie qui fait que le satellite quitte une orbite circulaire pour prendre d’abord la forme d’une orbite elliptique, puis parabolique puis enfin hyperbolique. En effet, un mouvement képlérien est à énergie constante. Donc ici, il y a bien consommation, restitution d’énergie surtout par le fait que l’extension du filin se fait à l’apogée.

C’est le moteur qui enroule/déroule le filin qui fournit cette énergie.

Figure 1

- Au bout de combien de temps, l’effet sur l’orbite est non réversible. Si le temps de simulation est trop long par rapport à votre puissance de calcul, jouer sur un paramètre de l’énoncé pour raccourcir considérablement ce temps.

L’équation du mouvement est :

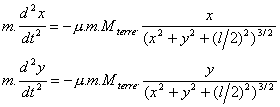
La simulation consistera à faire varier l entre 0 au périgée et l=100 km à l’apogée suivant une fonction de variation en escalier (le temps d’enroulement ou de déroulement du filin est négligeable devant le temps d’une révolution du satellite).

L’effet sera non réversible dès que l’orbite, de circulaire devient parabolique et de parabolique à elliptique. Un bon moyen de suivre cette évolution est de calculer l’excentricité de la trajectoire. Cependant, calculer l’excentricité à partir de l’intégration numérique de la trajectoire n’est pas une sinécure….Il y a plus simple : seule l’ellipse admet un point où l ‘éloignement au centre de la terre admet un maximum. C’est d’ailleurs ce qu’on exploite dans la fonction @events pour étendre/rétracter le filin qui joint les deux extrémités du satellite haltère.

Dans le code, on dérive tout simplement la fonction et on teste si elle est égale à zéro (et dans ce cas, quand ?):

Dans le cas d’une hyperbole ou d’une parabole, cette dérivée n’égale jamais zéro. La fonction @events ne provoque jamais l’arrêt de l’intégration et la condition t(end)==t_init+Periode à condition toutefois qu’on ne force pas le pas d’intégration sinon, impossible de respecter cette égalité du fait des erreurs d’arrondi ; donc

[t_init t_init+Periode]

est OK mais

[t_init :1 : t_init+Periode]

N’est pas bon

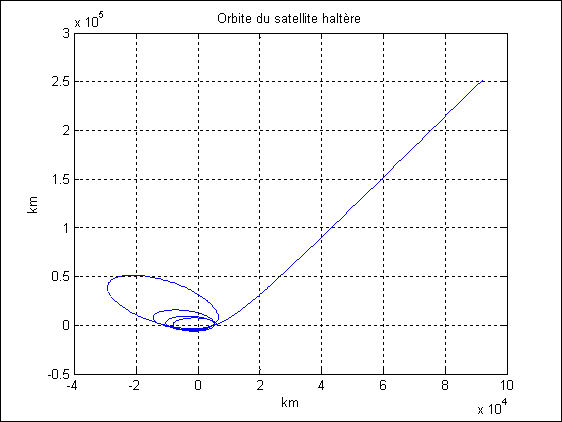
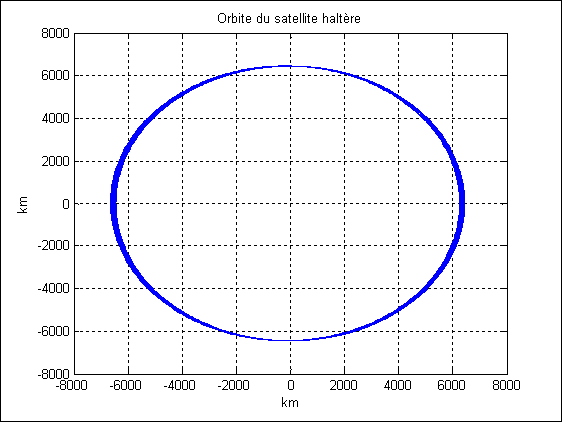
La Figure 2 et la Figure 3 donnent le résultat pour un filin de 2000 km de long (ce qui est irréaliste mais qui raccourcit le temps de calcul) : on voit qu’en un peu moins de 0.6 jours, le satellite passe pour la dernière fois par son apogée. Lorsqu’il va aborder sa nouvelle orbite après extension/rétraction du filin, il part vers l’infini. Mais un autre problème apparaît. Du fait que le périgée décroît, le satellite va s’écraser sur la Terre s’il part d’une orbite à 100 km d’altitude (voir Figure 3).

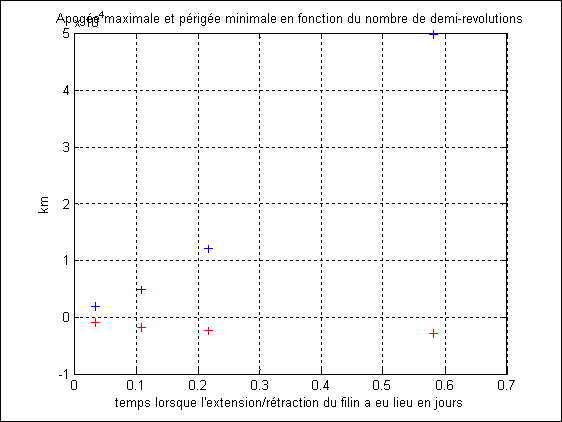
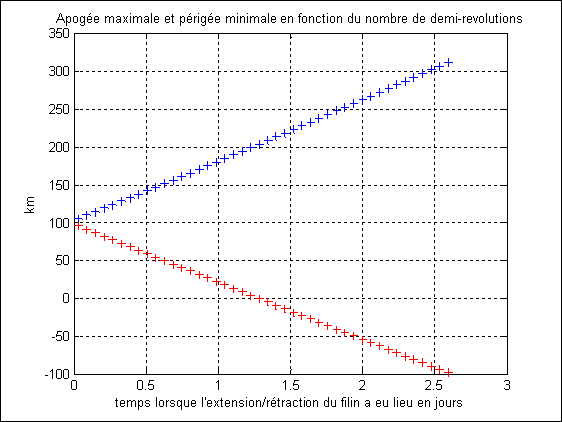
La Figure 4 et la Figure 5 montrent l’effet de l’extension/rétraction du filin si le satellite haltère part de 100 km d’altitude. Un problème pratique est, comme nous l’avons dit ci-dessus, que le périgée décroît de sorte que le satellite finit par s’écraser sur la terre (en fait dès 90 km d’altitude les équations ne sont plus correctes puisque le ralentissement atmosphérique devient non négligeable). L’évolution de l’altitude maximale et minimale sur la Figure 5 permet de mieux comprendre le problème : le périgée décroît dans la même proportion que l’apogée croît. Cela permet d’imaginer une stratégie pour éviter de frotter les couches hautes de l’atmosphère ; on donne une vitesse initiale au satellite qui le force à avoir une orbite plus elliptique.

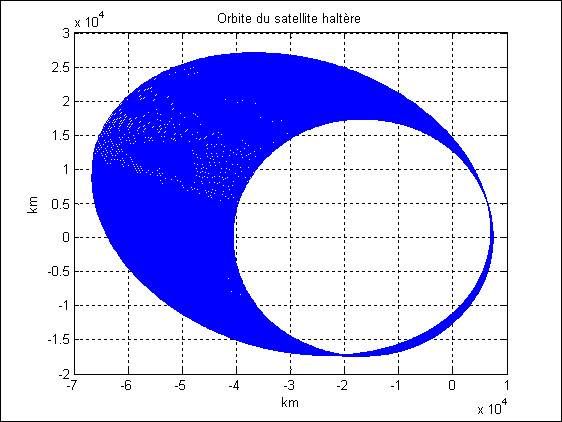
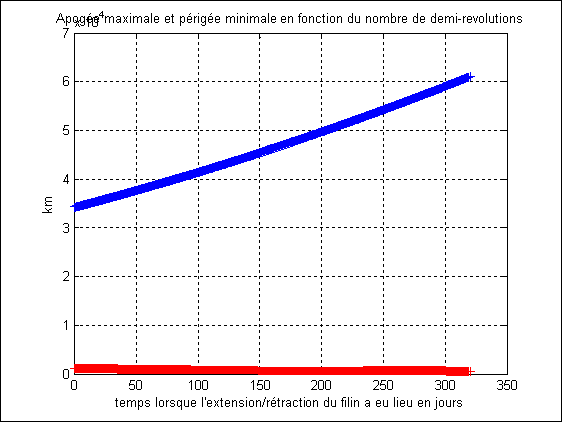
C’est ce que montrent les Figure 6 et Figure 7 : j’ai arrêté la simulation après 1098 orbites c’est-à-dire après presque 1 an de trajectoire et le satellite haltère n’avait toujours pas frappé les couches hautes de l’atmosphère. Il faut dire aussi que j’ai pris une vitesse initiale de 30 % supérieure à la première vitesse cosmique (celle qui donne une orbite circulaire) et l’altitude initiale est de 1100 km au lieu de 100km.

Pour bien faire, il faut voir si effectivement le satellite arrive à passer à une orbite parabolique. L’étudiant doit trouver une bonne combinaison de vitesse initiale et d’altitude initiale pour faire échapper en effet le satellite haltère de l’attraction terrestre. Il faut en outre que la vitesse initiale choisie reste inférieure à le deuxième vitesse cosmique (qui fait échapper d’office le satellite à l’attraction de la Terre) pour qu’il y a en effet un gain.

Figure 6

Figure 7

Le code suivant arrête l’exécution lorsque un extremum est rencontré (on est donc au périgée ou à l’apogée) est on provoque alors une extension/rétraction du filin.

clear

echo off

global mu l

mu=39.86*10000;

longueur=100;step=1;

options = odeset('Events',@events,'RelTol',1e-8)

Periode=sqrt(4*pi^2/mu*10447^3)*100;

x_init=10447;y_init=0;dx_init=0;dy_init=sqrt(39.86*10000/10447)*1;t_init=0;

figure(1);

Title('Orbite du satellite haltère');hold on;grid on;box on;

xlabel('km');

ylabel('km');

hold on;

figure(2);

Title('Apogée maximale et périgée minimale en fonction du nombre de demi-revolutions');hold on;grid on;box on;

xlabel('temps lorsque l''extension/rétraction du filin a eu lieu en jours');

ylabel('km');

hold on;

for j=1:6000;

display(num2str(j))

l_old=l;

l=longueur*(1+step);

step=step*(-1);

[t,y]=ode45(@vrai_gravidyne_eq, [t_init t_init+Periode],[x_init y_init dx_init dy_init],options);

if mod(j,2)==0

figure(2);line(t_init/(3600*24),max(sqrt(y(:,1).^2+y(:,2).^2))-6347,'Marker','+');

line(t_init/(3600*24),min(sqrt(y(:,1).^2+y(:,2).^2))-6347,'Marker','+','Color','r');

drawnow;

if (min(sqrt(y(:,1).^2+y(:,2).^2))-6347<90)

display('ralentissement atmosphérique')

break

end

figure(1);plot(y(:,1),y(:,2));hold on;

if t(end)==t_init+Periode

display('stop');drawnow;

break;

end

x_init=y(end,1);

y_init=y(end,2);

dx_init=y(end,3);

dy_init=y(end,4);

t_init=t(end);

end

function [value,isterminal,direction] = events(t,y)

value = (y(1)*y(3)+y(2)*y(4)); % Detect height = 0

isterminal = 1; % Stop the integration

direction = 0; % Negative direction only

function dy = vrai_gravidyne_eq(t,y)

global l mu

dy = zeros(4,1);

dy(1) = y(3);

dy(2) = y(4);

dy(3)=-mu*y(1)/(y(1)^2+y(2)^2+l^2/4)^(3/2);

dy(4)=-mu*y(2)/(y(1)^2+y(2)^2+l^2/4)^(3/2);

- Comment pourrait-on selon vous exploiter cet effet dans l’exploration des planètes proches mais quel est l’élément contraignant ?

Le temps d’échappement à l’attraction terrestre pour un satellite haltère dont les deux extrémités sont reliées par un filin de 100 km est très long rendant cette méthode d’exploration du système solaire proche peu réaliste. Cependant, on pourrait imaginer ce type d’échappement de l’attraction d’une planète plus massive comme Jupiter.

- Quelle est l’influence de l’orbite initiale sur la manifestation de cet effet (influence de l’altitude et de l’excentricité de l’orbite)

Il faut donc avoir mis en évidence le problème du ralentissement atmosphérique et le fait que une orbite circulaire de départ augmente ce risque de taper les couches hautes de l’atmosphère.

Le code matlab ci-après donne la simulation montrée sur l’énoncé on line du projet.

Clear

echo off

global mu l

mu=39.86*10000;

longueur=50;step=1;

options = odeset('Events',@events,'RelTol',1e-6)

aviobj = avifile('c:\projet001.avi','quality',100,'fps',25)

aviobj.Quality = 100;

vitesse_initiale_200km_altitude_en_orbite_circulaire=sqrt(39.86*10000/6447);

Periode=sqrt(4*pi^2/mu*6447^3)*10;

x_init=6547;y_init=0;dx_init=0;dy_init=sqrt(39.86*10000/6447)*1.1;t_init=0;

%h=figure('NumberTitle','off','Name','Projet 1 - 2005-2006','Position',[30 35 300 300])

%Title('Orbite du satellite haltère');hold on;grid on;box on;

%axis([-14000 14000 -14000 14000])

hh=figure('NumberTitle','off','Name','Projet 1 - 2005-2006','Position',[335 35 300 300],'Color','w');

Title('Mouvement Temps Proportionnel du satellite ');hold on;

view([0.55,0.75, 0.45]);hold on;box on; grid on;

axis([-14000 14000 -14000 14000 -longueur longueur])

zlabel('Service CFAO FSA - ULB - Anne Academique 2005-2006','FontSize',8)

xx=[0 0];

yy=[0 0];

zz=[0 0];

xx_old=xx;yy_old=yy;zz_old=zz;

q=line('XData',xx,'YData',yy,'ZData',zz);

s=line('XData',xx,'YData',yy,'ZData',zz);

u=line('XData',xx,'YData',yy,'ZData',zz);

v=line('XData',xx,'YData',yy,'ZData',zz);

l=longueur*(1+step)

%figure(h);

for j=1:1;

l_old=l;

l=longueur*(1+step);

step=step*(-1);

[t,y]=ode45(@vrai_gravidyne_eq, [t_init:10:t_init+Periode],[x_init y_init dx_init dy_init],options);

xx=[y(1,1) y(1,1)];

yy=[y(1,2) y(1,2)];

zz=[-l/2 l/2];

for i=1:5:max(size(y))

xx_old=xx;

yy_old=yy;

zz_old=[-l_old/2 l_old/2];

xx=[y(i,1) y(i,1)];

yy=[y(i,2) y(i,2)];

zz=[-l/2 l/2];

set(v,'XData',0,'YData',0,'ZData',0,'Color','b','LineWidth',2,'Marker','o','Markersize',10);

set(q,'XData',xx,'YData',yy,'ZData',zz,'Color','r','LineWidth',1);

set(s,'XData',xx(1),'YData',yy(1),'ZData',zz(1),'LineWidth',10,'Marker','o','Color','r');

set(u,'XData',xx(2),'YData',yy(2),'ZData',zz(2),'LineWidth',10,'Marker','o','Color','r');

F = getframe(gcf);

aviobj = addframe(aviobj,F);

drawnow;

end

%figure(h);

%plot(y(:,1),y(:,2));hold on;

figure(hh);