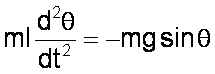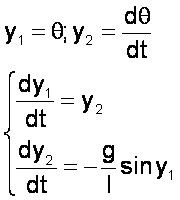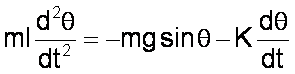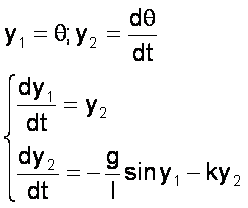|
Modéliser le mouvement d’un pendule simple de
masse m=1 kg avec Matlab et visualiser en temps
quasi réel son mouvement. Tracer les trajectoires dans le plan des phases.
Dans un premier temps, on modélisera le pendule
sans frottement visqueux(damping)
puis avec un frottement visqueux de type
k.dq/dt avec k=1/s.
Equation du Mouvement
Modélisation Matlab
Le code Matlab
Le frottement visqueux
Les animations
Vers le TP 1
Vers le Tutorial 2 (double-pendule)
Equation
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
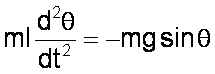
Modélisation Matlab
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Tout comme avec
Runge Kutta, on est d’abord amené à ramener l’équation
différentielle du mouvement qui est au
second ordre en un système d’équations différentielles du premier
ordre :
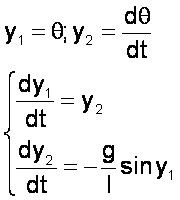
Code Scilab – Mouvement du pendule 
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
function dy=fon(t, y) global g l dy(1) = y(2); dy(2)=-g/l*sin(y(1)); endfunction teta_init = 45;teta_init=teta_init/180*pi;dteta_init = 0; g=9.81;l=1; t=0:0.1:20; y=ode([teta_init;dteta_init],0,[t],fon); //Preparation du graphe f = gcf(); // on r�ecup�ere le handle de la fen^etre graphique f.pixmap = "on"; // on met la fenetre en mode double buffer f.background = color("white");f.foreground = color("white");;//FIN Preparation du graphe i = 1; while i<=length(y) i = i+1; clf(); // On efface l'image précédente - on évite le scintillement xtitle('', 'm', 'm'); a = gca(); // On récupère l'objet graphique axes pour modifier les légendes a.isoview = "on"; a.data_bounds = [-2 2 -2 2]; a.title.text = "Le pendule "; a.title.font_size = 4; a.title.foreground = color("white"); a.background = color("white");; xpoly([0 +l*sin(y(1,i))],[0 -l*cos(y(1,i))],"lines",0) ep = gce(); // On récupère l'objet graphique double-pendule atwood // pour modifier son aspect cosmétique ep.thickness = 3;ep.foreground = color("blue"); plot([+l*sin(y(1,i))],[-l*cos(y(1,i))],'o','MarkSize',10,'MarkBackground','b') xgrid(12) show_pixmap() // basculement de la pixmap �a l'�ecran end f.pixmap = "off"; // on remet la fen^etre en mode usuel
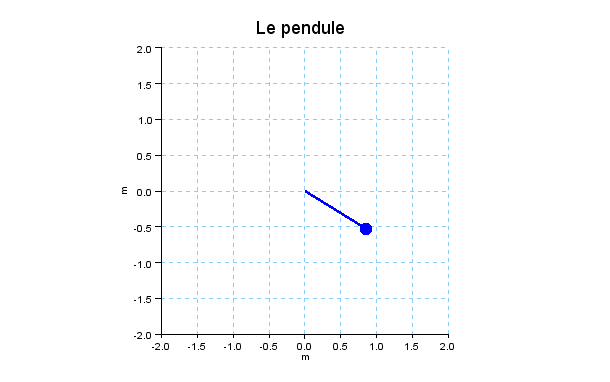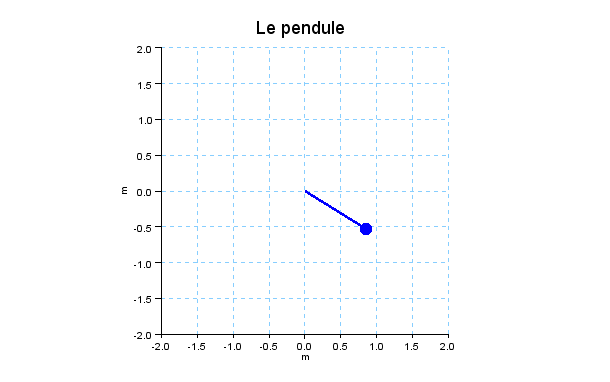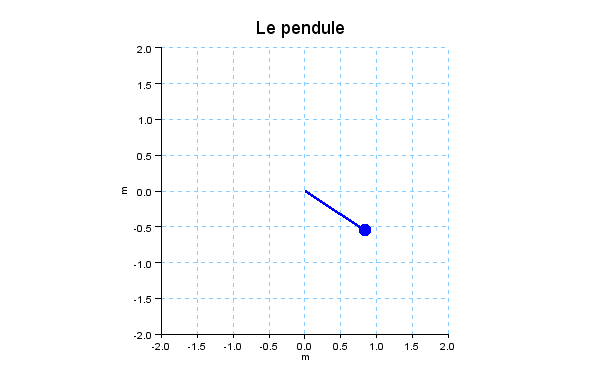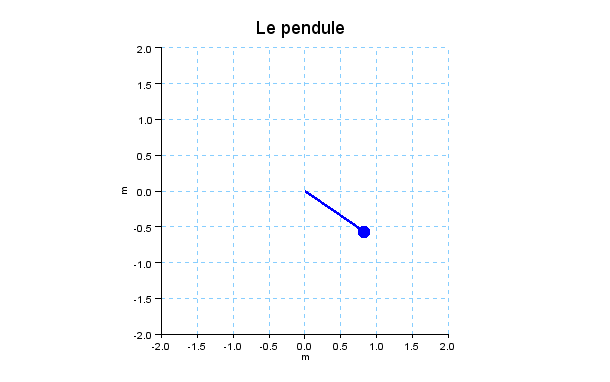
Si on veut suaver les images de l’animation pour en faire un film,
ajouter :
f.pixmap="off" filename = sprintf("R:\image%d.gif", i);xs2gif(f,filename);
Code Matlab – Plan des Phases
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
clear;
mov = avifile('c:\test113.avi','Compression','None','Quality',100,'fps',25)
global g l
l=10;g = 9.81
figure('NumberTitle','off','Name','Cours
du 29.11.2002')
axis([-6 20 -6
6]);hold on;
xlabel('\theta ');
ylabel('d\theta/dt /s');
for i=1:100
options = odeset('RelTol',1e-5);
[t,y] = ode45('Linear_Damping_Pendulum',[0:0.05:20],[i/5
0],options);
plot(y(:,1),y(:,2));
% Sauvetage sous forme de film
F = getframe(gcf);
mov = addframe(mov,F);
% Fin
% Sauvetage sous forme d’une sucession
d’images png
X =
frame2im(F);
imwrite(X,['R:\pendule',num2str(i),'.png'],'png')
drawnow;
% Fin
zoom on
hold on;
end
mov = close(mov);
function dy = Linear_Damping_Pendulum(t,y)
global g l k L
dy = zeros(2,1);
dy(1) = y(2);
dy(2)=-g/l*sin(y(1));
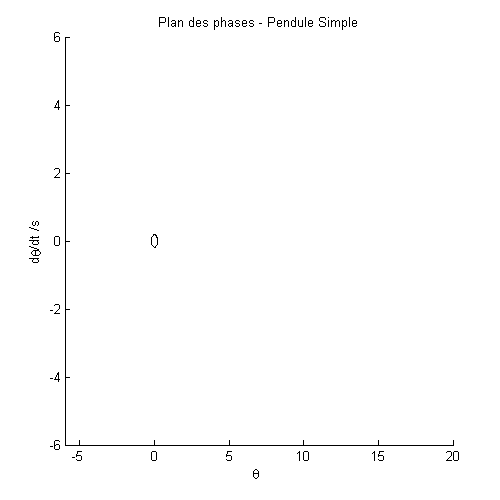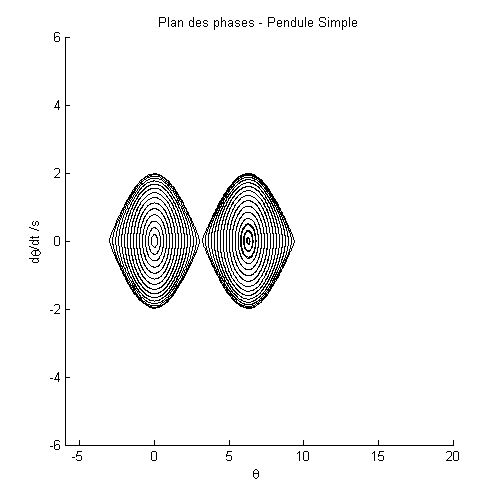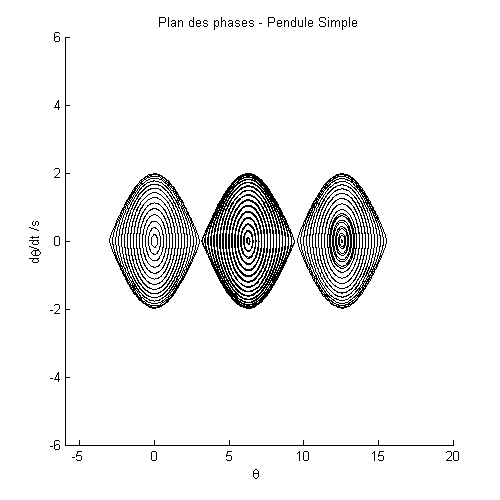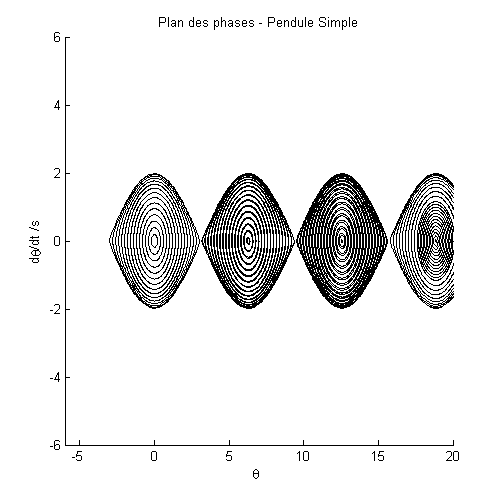
Retour haut de la page
Simulation Temps Quasi Réel du
mouvement
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Code Matlab
clear;
mov = avifile('c:\test55.avi','Compression','Indeo5','Quality',100,'fps',25)
global g l k
l=10;g = 9.81;k=0;
figure('NumberTitle','off','Name','Cours
du 18.02.2005','Renderer','OpenGL','Color','w','Position',[100 100 500 500])
subplot(2,1,1,'replace');axis([-22 22
-11 11]);box on;
Title('Simulation du Mouvement');hold on
subplot(2,1,2);axis([-6 20 -6
6]);
Title('Plan des
Phases');xlabel('\theta');ylabel('d\theta/dt /s');hold on
options = odeset('RelTol',1e-6);
for j=1:15
[t,y]
= ode45('Linear_Damping_Pendulum',[0:0.25:10],[0 j/5],options);
x=zeros(2,1);
z=zeros(2,1);
for i=2:max(size(t))
tic
x(2)=l*sin(y(i,1));
z(2)=-l*cos(y(i,1));
subplot(2,1,1,'replace'); axis([-22 22
-11 11]);box on;grid on;
line(x,z,'LineWidth',2);
line(x(2),z(2),'Marker','.','MarkerSize',40');
subplot(2,1,2);line([y(i-1,1)
y(i,1)],[y(i-1,2) y(i,2)],'Color','r','LineWidth',1);
F = getframe(gcf);
mov = addframe(mov,F);
drawnow;
while toc<0.0025;end; % le
mouvement est accéléré 100 fois
end
end
mov = close(mov);
(Animation réalisée avec Scilab  ) )
Le pendule est
lancé avec un vitesse initiale de plus en plus grande
à partir de sa position d’équilibre stable 0°. Le mouvement est en temps
réel.
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Code Scilab 
function dy=Linear_Damping_Pendulum(t, y) global g l k L dy(1) = y(2); dy(2)=-g/l*sin(y(1)); endfunction l=10;g = 9.81;k=0; //Preparatif d'affichage f = gcf(); // on recupere le handle de la fenetre graphique f.pixmap = "on"; // on met la fenetre en mode double buffer f.background = color("white");f.foreground = color("white");//FIN Preparatif d'affichage //Preparatif d'affichage de la première sous-fenêtre subplot(2,1,1); a = gca(); // on recupere le handle des axes pour améliorer leur cosmétique a.isoview = "on"; a.data_bounds = [-22 22 -11 11]; a.title.text = "pendule"; a.title.font_size = 4; a.title.foreground = color("white");;a.background = color("white"); //On prépare la barre du pendule puis on récupère le handle pour améliorer sa cosmétique ep1=xpoly(x,z,"lines",0); ep1 = gce(); ep1.thickness = 3; ep1.foreground = color("blue");//FIN On prépare la barre du pendule puis on récupère le handle pour améliorer sa cosmétique //On prépare l'extrémité du pendule puis on récupère le handle pour améliorer sa cosmétique ep2= xrect(x(2),z(2),2,2) ep2=gce(); ep2.thickness = 2; ep2.foreground = color("blue");show_pixmap() //FIN On prépare l'extrémité du pendule puis on récupère le handle pour améliorer sa cosmétique //Preparatif d'affichage de la seconde sous-fenêtre subplot(2,1,2) a = gca(); a.box="on"; a.x_location="middle"; a.isoview = "on"; a.data_bounds = [-20 20 -5 5]; a.title.text = "Plan des phases"; a.font_size = 3; // taille de la police a.title.foreground = color("white");;a.background = color("white");a.x_location = "origin"; // top, bottom, middle ou origin a.y_location = "origin"; // left, right, middle ou origin a.axes_visible = 'on' ; // visibilité des axes a.x_location="bottom"; // top, bottom, middle ou origin a.y_location="left"; // left, right, middle ou origin a.box="on"; // on, off, hidden_axes a.title.font_size=3; //FIN Preparatif d'affichage de la seconde sous-fenêtre x=zeros(2,1); z=zeros(2,1); for j=1:15 // On trace 15 trajectoires de phases correspondant à 15 CI différentes t=0:0.25:10; y = ode([0;j/5],0,[t],Linear_Damping_Pendulum); for i=2:max(size(t)) subplot(2,1,1); x(2)=l*sin(y(1,i)); z(2)=-l*cos(y(1,i)); ep1.data=[x,z]; ep2.data=[x(2),z(2),2,2]; subplot(2,1,2); xtitle('', 'theta', 'dtheta/dt'); xpoly([y(1,i-1) y(1,i)],[y(2,i-1) y(2,i)],"lines",0); xgrid(12) i = i+1; show_pixmap() // basculement de la pixmap �a l'�ecran // Pour sauver l'naimation en sucesssion de GIF // f.pixmap="off" // on sort du mode double buffer pour l'animation // filename = sprintf("R:\image%d.gif", j*100+i) // xs2gif(f,filename); // FIN Pour sauver l'naimation en sucesssion de GIF end end
Animation réalisée avec Scilab 
Retour haut de la page
Effet
du Damping
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
On introduit un frottement
visqueux
L’équation du pendule est
alors :
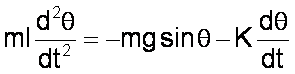
Et la modélisation Matlab
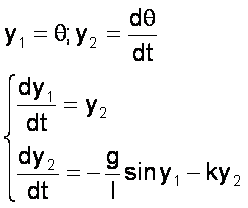
Dans les codes
précédents il suffit de changer :
function dy = Linear_Damping_Pendulum(t,y)
global g l k L
dy = zeros(2,1);
dy(1) = y(2);
dy(2)=-g/l*sin(y(1))-k*y(2);
Le mouvement
est accéléré.
Retour haut de la page
|