Sciences
Appliquées

 |
Faculté des Sciences Appliquées  |
Exercices des 12 et 18/11/99 |
Séance n° 8 : Fonctions vectorielles
| 1. | 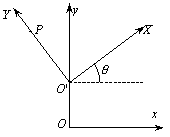 |
Soit t
une variable scalaire. On considère un repère Oxy fixe, ainsi qu’un second repère mobile (dépendant de la variable t) O'XY. Ce dernier repère est défini de la façon suivante :
On considère également un point P sur l'axe OY, dont la position varie avec t, tel que :
|
| On
définit ensuite les deux fonctions vectorielles :
|
||
| 2. | 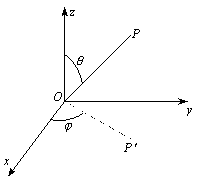 |
Soit la
courbe C, lieu des points P, définis en
coordonnées sphériques en fonction de la variable t
par :
avec k > 0 (constante) Cette courbe est l’hodographe de
la fonction ( [0,2p/k)] ® V ).
|
| Déterminer
les vecteurs dérivée première Calculer et représenter sur la courbe C les vecteurs obtenus en d) lorsque j = 0. |
||