 |
Faculté
des
Sciences
Appliquées
|
Mécanique
Rationnelle
2e candidature 1999-2000 Corrigé de la séance n° 6 |
|
L’
équation du mouvement (voir cours) s’écrit :
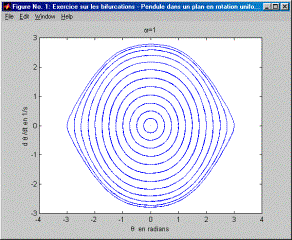
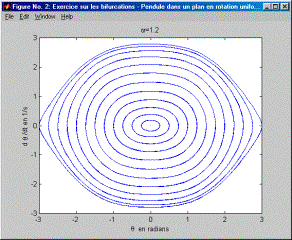
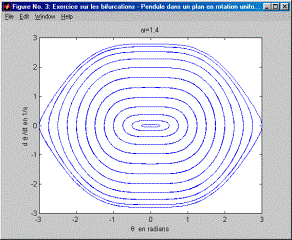
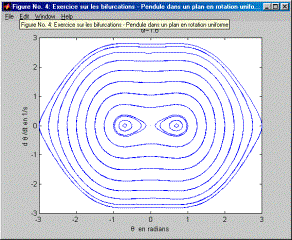
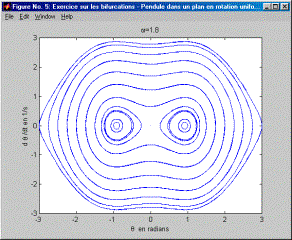
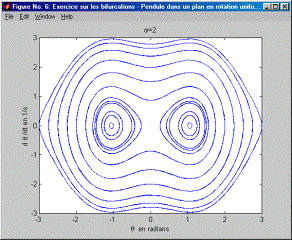
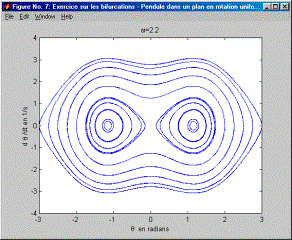
On notera au préalable que ce mouvement est celui d'un pendule de rayon r et de masse m dont le plan du mouvement est en rotation. Il s’agit bien d’une équation positionnelle (qui ne dépend que de la position) pour laquelle l’étude dans le plan des phases s’avère aisée. On a vu au cours qu’à partir d’une certaine valeur de w une bifurcation apparaissait. Le but de cet exercice est d’examiner l’évolution des trajectoires dans le plan des phases depuis w =0 jusqu’à et au-delà de la valeur de w où apparaît une bifurcation à partir de laquelle deux points d’équilibre stable et non plus un point unique d'équilibre stable apparaissent. Le code Matlab pour résoudre l’équation est donné ci-après. Le résultat de ce code donne les 7 diagrammes qui suivent et pour lesquels w croît par incrément de 1/5 s. : on note très bien l’évolution des trajectoires dans le plan des phases. Pour w=1/s (Figure 1), on obtient des trajectoires dans le plan des phases qui ne sont pas sans rappeler les trajectoires dans le plan des phases d’un pendule simple sans rotation. Il y a un seul point d’équilibre : q=0°. En d’autres termes, la valeur de w n’est pas suffisamment grande pour que le comportement s’éloigne de celui d’un pendule simple sans rotation. Ensuite, au fur et à mesure que w augmente (Figure 2 à Figure 7), on note que les trajectoires du plan des phases s’étirent et subissent un pincement autour d’un axe de symétrie d’équation q =0°. Au-delà de w=1.4/s (Figure 3) et en deça de w =1.6/s (Figure 4), on passe par la bifurcation (on laisse à l’étudiant de trouver la valeur exacte de w où se produit la bifurcation). Dans le plan des phases, cela se traduit par un pincement si prononcé des trajectoires qu'apparaissent deux nouveaux centres autour desquelles les trajectoires tournent. Ces deux points d'équilibre stable remplacent le premier point singulier d’équilibre en dq/dt=0 et q=0°. Ce dernier se transforme d'ailleurs en point d'équilibre instable (on voit, en effet, que la trajectoire démarrant aux conditions initiales: q=0 dq/dt=0 reste un point; en utilisant l'instruction comet[1] pour dessiner les trajectoires dans le plan des phases, on noterait également que les trajectoires s'approchant du point q=0 dq/dt=0 s'en éloignent aussitôt). Il est remarquable que la visualisation de l’évolution des trajectoires dans le plan des phases montre l’arrivée progressive de la bifurcation par le pincement de plus en plus prononcé des trajectoires. Un diagramme donnant les positions d’équilibre qen fonction de w montre certes la bifurcation (voir cours) mais la laisse entourée d’un halo de mystère puisque le diagramme subit en un point donné un dédoublement sans que rien au préalable, dans l’allure de la courbe, n’ait pu la laisser présager. Sachant que les trajectoires correspondant à différentes conditions initiales ne peuvent se couper dans le plan des phases, quelle autre évolution qu’un pincement aurait pu avoir lieu ? C’est aussi un peu notre chance puisque ce pincement laisse apparaître progressivement la venue de la bifurcation. L’apparition de la bifurcation est, dans ce cas, aisée à comprendre intuitivement. Si on imagine un pendule au repos dont le plan du mouvement entre en rotation rapide, la force centrifuge aura pour effet de dévier cette position de repos de la verticale. Toutefois, la bifurcation a ceci de remarquable qu’il faut que la force centrifuge atteigne un certain seuil pour que q=0 ne soit effectivement plus une position d’équilibre.
|
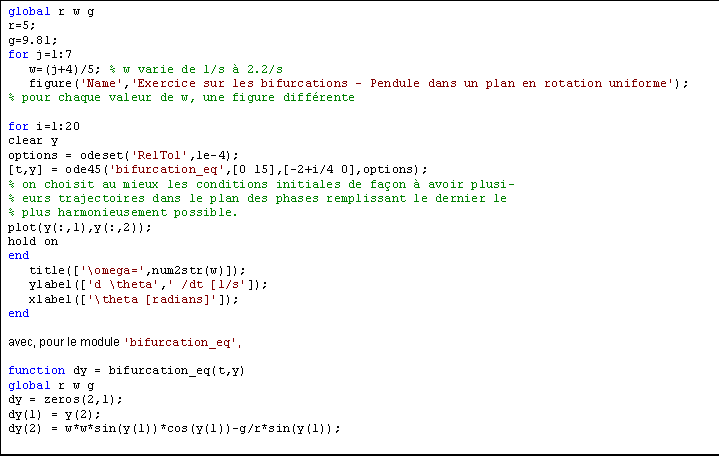
Figure 0: Code Matlab
[1] Cette instruction permet de visualiser le dessin de la trajectoire et donc, de se rendre compte si cette dernière s'approche ou s'éloigne des points singuliers duplan des phases.