Faculté des  Sciences  Appliquées

Mécanique Rationnelle 1e candidature 1999-2000 Corrigé de la séance n° 20

Exercice: Voyage vers la Lune (Problème des trois corps) Equation du Mouvement Choix particulier d'un système d'unités Résolution numérique Analyse des résultats Quelques compléments sur le problème à 3 et à n corps  On souhaite envoyer une sonde, placée sur une orbite parking à 100 km d'altitude, vers la Lune. On demande la vitesse minimale ( vitesse v ) que doit déployer le moteur de la sonde pour pouvoir atteindre la Lune ainsi que la position (angle a ) sur l'orbite circulaire où le moteur doit démarrer. On considérera que la Lune est animée d'un mouvement de rotation autour de la Terre de période 27.32 jours (mois sidéral). Figure 1 Solution: Equation du mouvement Il est naturel de prendre comme origine des axes la Terre et de décrire le mouvement de la sonde et de la Lune par rapport à cette origine. En effet, le suivi du mouvement de la sonde se fait à partir de la salle de contrôle sur la Terre. Le fait de prendre comme origine des axes la Terre, elle-même partie prenante du problème des trois corps et animée d'un mouvement, va donner une équation du mouvement de la sonde peu intuitive. C'est le tribut à payer au fait que l'origine des axes est non inertielle. Voyons ce que donne l'équation du mouvement de la sonde dans le système Terre-Lune-Sonde en prenant la Terre comme origine. Pour ce faire, commençons par écrire le mouvement des 3 corps qui s'attirent mutuellement dans un référentiel absolu.  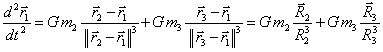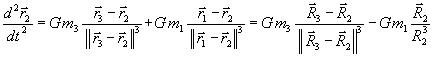Figure 2 L'équation du mouvement de la masse m1 s'écrit: L'équation du mouvement de la masse m2 s'écrit: En soustrayant la première équation de la seconde, on obtient: (1) De même: (2) Ces deux dernières équations décrivent le mouvement des masses m2 et m3 relativement à m1 puisque en résolvant (1) et (2), on obtient respectivement la loi de variation de R2 et de R3 qui sont la position de m2 et de m3 par rapport à m1. Ces équations ne sont pas intuitives: cela tient au fait que l'origine des axes (la Terre) n'est pas au repos. Dans la suite de l'exercice, on considérera que m1=Terre, m2=Lune animé d'un mouvement circulaire uniforme autour de la Terre (période de rotation: 27.32 jours) et on ne gardera finalement que l'étude de l'équation (2) qui décrit le mouvement de la sonde de masse m3. On supposera que le mouvement de la Lune autour de la Terre et le mouvement de la sonde sont coplanaires de sorte qu'on peut se limiter à transformer l'équation vectorielle (2) en deux équations scalaires.   Choix particulier d'un système d'unités On se propose de travailler dans un système d'unités particulier: L'unité de masse sera la masse de la Terre. Ainsi, m1=1 et m2=1/81.3 L'unité de distance est la distance Terre-Lune L'unité de temps sera choisie de sorte que la valeur numérique de la constante de gravitation soit égale à l'unité. Pour ce faire, on utilise la troisième loi de Kepler: Ce choix particulier de système d'unités permet de travailler sur des nombres de grandeur raisonnable et d'éviter ainsi les erreurs d'arrondi tout au long des calculs. Il est très fréquent, d'ailleurs en astronomie du système solaire de prendre le demi grand axe de l'orbite de la Terre autour du Soleil comme unité de longueur.  Il est tout aussi fréquent d'essayer de rendre les équations adimensionnelles en les normalisant ou, comme ici, de choisir un systèmes d'unités ad hoc, afin d'éviter les erreurs d'arrondi en cas de résolution numérique. Si deux corps de masses m1 et m2 tournent l'un autour de l'autre en une orbite elliptique de demi grand axe a, alors la période de révolution (c'est-à-dire le temps minimum pour qu'une même configuration se répète) est donnée par: (3) Dans le cas du système Terre/ Lune, on sait que P est un mois sidéral, c'est-à-dire: 27.32 jours. D'autre part, on sait que m1=1 et m2=1/81.3. On sait enfin que a=1 (puisque la distance Terre-Lune est choisie comme unité de longueur). On pose donc G=1 dans (3). Donc, par une règle de trois: 27.32 jours correspondent à unités de temps Donc 1 heure correspond à unités de temps . Donc, 1 heure dans le temps terrestre vaudra dans notre choix de système d'unités: 1*(2*pi)/(27.321662*24) unités de temps. Plus particulièrement une unité de temps dans notre système d'unités correspond à 4.375 jours.  Sachant que la distance Terre-Soleil représente 384 400 km, l'unité de vitesse dans notre système d'axes correspond à 1.017 km/sec.   Résolution numérique Considérons qu'au moment où les moteurs de la sonde sur son orbite parking s'enclenchent, la Lune est sur l'axe x à une distance 1 de la Terre ainsi que représenté sur la Figure 1. 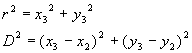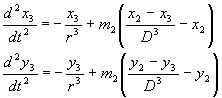Le mouvement de la Lune peut alors être décrit par les équations: x2 =cos(n.t); y2=sin (n.t) où n/2p = P =(1+M)1/2 On pose: L'équation (2) devient scalairement: Le code Matlab qui implémente ces équations est:  global MoonMass MeanMotion t_final; clear t; clear y; % L'orbite parking est de 100 km Altitude=100; % On doit trouver le bon Alpha pour que la sonde arrive sur la Lune Alpha=-39*pi/180; MoonMass=0.0123; MeanMotion = sqrt(1+MoonMass); options = odeset('RelTol',1e-8); % Le mouvement de la sonde est calculé jusqu'à 100 heures après que la sonde  % a quitté son orbite parking % On sauvegarde toutes les heures la position et la vitesse de la sonde. % 0.9834 est le facteur qui permet de convertir des km/s en l'unité de  % vitesse qui découle du choix particulier de notre système d'unités (dist.  % Terre- Lune= 1 etc...) [t,y] = ode45('moontrip_eq',[0:1*(2*pi)/(27.321662*24):1000*(2*pi)/(27.321662*24)],[(Altitude + 6378)/384400*sin(Alpha) -(Altitude + 6378)/384400*cos(Alpha) 11*0.9834*cos(Alpha) 11*0.9834*sin(Alpha)],options); % Les 1000 points d'intégration sont affichés à raison d'un point toutes  % les 0.1 secondes. Les trajectoires de la Lune et de la Sonde autour de  % la Terre sont donc simulées en temsp réel avec comme base de temps 0.1s  % de simulation = 1 heure dans la réalité. for i=2:1000 plot(cos(MeanMotion*t(i)),sin(MeanMotion*t(i)),'b+'); tic while toc<0.1;end; plot(cos(MeanMotion*t(i-1)),sin(MeanMotion*t(i-1)),'w+');  hold on; plot(y(i-1:i,1),y(i-1:i,2)); axis([-2 2 -2 2]); end hold off; % Sauvegarde sur le fichier MoonTrip.txt de la position de la sonde et la  % Lune toutes les heures. fid = fopen('c:\MoonTrip.txt','w'); fprintf(fid,'temps heure; x_sonde ; y_sonde ; x_lune ; y_lune \n'); final=size(t); for i=1:final(1,1) fprintf(fid,'% 6.4f ; % 6.4f ; % 6.4f ; % 6.4f ; % 6.4f\n',t(i) /(2*pi)*(27.321662*24),y(i,1),y(i,2),cos(MeanMotion*t(i)),sin(MeanMotion*t(i))); end fclose(fid); hold off; Le module moontrip_eq.m est donné par function z = moontrip_eq(t,y) global MoonMass MeanMotion t_final; z = zeros(4,1); r = sqrt(y(1)*y(1) + y(2)*y(2)); rrr = r*r*r; z(1) = y(3); z(2) = y(4); xm = cos(MeanMotion*t); ym = sin(MeanMotion*t); d = sqrt((y(1) - xm)*(y(1) - xm) + (y(2) - ym)*(y(2) - ym)); z(3) = - y(1)/rrr + MoonMass*((xm - y(1))/(d*d*d) - xm); z(4) = - y(2)/rrr + MoonMass*((ym - y(2))/(d*d*d) - ym); La Figure 3 montre ce que fait le code ci-dessus: il simule en temps quasi réel le mouvement de la Sonde et de la Lune (sous forme d'un signe +) autour de la Terre pris comme point de référence et située en (0,0). La Figure 3 montre la position de la Lune et la trajectoire de la Sonde après 1000 heures. Figure 3   Analyse des résultats Pour déterminer la vitesse initiale minimale, on peut partir de l'équation donnant la vitesse de libération de l'attraction terrestre en négligeant l'influence de la Lune: V=(2mG/r0)1/2 c'est-à-dire dans notre choix de système d'unités: (2/ r0)1/2 On peut vérifier par le calcul numérique qu'on peut aller un petit peu en-dessous de cette valeur grâce à l'attraction de la Lune sur la sonde. Par simplification, on prendra v =11 km/s  Pour a= - 39°, la sonde effectue un 8 entre la Terre et la Lune. C'est de cette manière que les premières sondes qu'on faisait revenir sur Terre approchaient de la Lune pour en tirer quelques photos. Dans le cas des capsules Apollo, l'équipage, au voisinage de la Lune, opéraient quelques manœuvres pour se mettre en orbite autour de la Lune et ne pas revenir immédiatement vers la Terre (Figure 4). Les Russes ont perdu beaucoup de sondes lunaires au début de leur programme spatial parce qu'ils 'n'arrivaient pas à calculer précisément les conditions initiales du mouvement . De ce fait les sondes étaient perdues dans le système solaire. Figure 4: Graphe obtenu à parti d'un traitement par tableur du fichier de résultat MoonTrip.txt Pour a= - 40.5°, la sonde s'écrase sur la Lune après 69 heures de temps de vol. Pour le vérifier, on sait que dans notre système d'unités, le rayon de la Lune vaut 0.0045. Il suffit de constater qu'au cours de la simulation D devient bien inférieur à 0.0045 pour conclure à l'écrasement. Pour a= - 43 ° (Figure 5), la sonde s'approche de la Lune mais pas suffisamment pour être capturée par elle. Au contraire, on observe un effet de catapulte, dit encore effet d'accélération gravitationnelle : grâce à son passage près de la Lune sous l'effet de son attraction, la sonde change d'orbite est subit une accélération. Ce type de manœuvre est très souvent utilisée lorsqu'on envoie des sondes dans le système solaire. Ainsi, avant d'attaquer véritablement son voyage, la sonde passe au voisinage de la Lune et y acquiert une vitesse bien supérieure à celle que lui a imprimée son moteur lorsque la sonde a décollé de son orbite parking. On utilise aussi très souvent le même effet d'accélération gravitationnelle au passage de Jupiter pour les voyages vers les planètes extérieures du système solaire. On regardera ce qui se passe pour des valeurs de a très différentes de celles qui précèdent pour v=11 km/s et pour des valeurs de v beaucoup plus élevées. Figure 5: Graphe obtenu à parti d'un traitement par tableur du fichier de résultat MoonTrip.txt   Quelques compléments sur le problème à 3 et à n corps - Utilisation dans les sciences et les sciences appliquées - La simulation du problème à n corps. Une des plus grandes frustrations de la physique mathématique est l'impossibilité de déterminer analytiquement le comportement de systèmes comprenant plus de deux particules.  Le problème à 3 corps, tel qu'illustré ci-dessus, est un des plus féconds de la mécanique. Dans les années 60, le mathématicien Henon mettait pour la première fois en évidence un comportement chaotique en mécanique analytique, et plus particulièrement en mécanique céleste et ce, en étudiant le problème à 3 corps par la méthode de Poincaré. Ce fut une révolution d'autant plus grande que la mécanique céleste connue pour ses mouvement séculaires et réguliers, était peu suspecte de donner naissance, surtout elle, à du chaos.  C'est ainsi qu'on soupçonne aujourd'hui le mouvement de certaines planètes du système solaire de montrer un comportement chaotique lorsqu'on change d'échelle de temps. Les problèmes à n corps, c'est-à-dire l'interaction (gravitationnelle, électromagnétique ou autre) de plus de trois corps entre eux ( n est souvent grand à très grand) se retrouvent dans de très nombreuses sciences lorsqu'il s'agit d'étudier des phénomènes de bases de ces disciplines: la pertinence de certaines théories cosmologiques, l'interaction entre galaxies sont des exemples tirés de l'astrophysique. Dans la physique des plasmas, le problème à n corps et ses méthodes de résolution permettent aux physiciens de modéliser le mouvements des électrons et des ions dans un champ électromagnétique. En dynamique moléculaire, on peut ainsi modéliser la trajectoire des molécules et mieux comprendre et modéliser certaines questions de la mécanique des fluides (rhéologie, simulation des écoulements viscoélastiques). En toute rigueur, le problème à n corps devrait être modélisé à l'aide de n équations différentielles du mouvement. Dès que n dépasse quelques dizaines, parfois centaines, une résolution numérique exacte du système est illusoire même avec les ordinateurs les plus puissants. Les scientifiques ont alors été amenés à développer des méthodes qui permettent de réduire le nombre d'équations à résoudre. La méthode particule/particule Dans cette méthode, pour chaque particule, on accumule les forces générées par l'interaction avec les particules voisines. Une fois celles-ci calculées, on intègre l'équation, comme si les particules voisines étaient fixes. On arrive en quelque sorte à découpler les équations du mouvement entre elles. Il est clair que cette méthode est d'autant moins rigoureuse que les particules voisines sont proches de la particule pour laquelle on procède à cette simplification de l'équation. En effet, plus la particule voisine est proche de la particule considérée, plus la force d'interaction (par exemple, la gravitation) est élevée et l'accélération subie par les deux particules aussi. Supposer la particule voisine au repos est donc d'autant plus inexact. Dans ce dernier cas, il faut alors prendre des pas d'intégration sur le temps très petits mais ce n'est qu'un pis-aller dans l'application de la méthode. Cette méthode est utilisée avec succès en astrophysique, plus particulièrement pour l'étude de la dynamique des galaxies (en particulier lorsqu'elles entrent en collision). Si la plupart des galaxies ont une forme spirale ou elliptique, certaines ont une forme irrégulière. Une simulation à n corps a démontré que ces formes particulières étaient tout simplement dues à des galaxies spirales ou/et elliptiques entrant en collision. La méthode de maillage Avec cette méthode, une grille ou un maillage est posé sur la région à simuler. Les masses des particules sont alors représentées sur le maillage sous forme de densité qui est interpolée aux sommets du maillage. Les forces sont calculées à partir du potentiel du maillage et sur cette base, la simulation est effectué. Cette méthode s'apparente bien évidemment à la méthode des éléments finis, laquelle est aussi utilisée pour la simulation du problème à n corps. La méthode de maillage n'est toutefois pas idéale lorsqu'il faut modéliser une répartition non uniforme des particules ou des rencontres entre groupes de particules (dit aussi systèmes corrélés). Au voisinage des zones à plus haute densité de particules, on raffine alors le maillage. Pour tenir compte des changement de géométrie à grande échelle du système à n particules (comme, par exemple, les ondes de choc), on utilise alors des techniques de maillage dynamique qui s'adaptent automatiquement au changement de configuration géométrique. La méthode symplectique C'est la méthode la plus proche de la mécanique classique: elle utilise une approche hamiltonienne à savoir la conservation de l'énergie et autres intégrales premières le cas échéant. On peut alors se permettre des pas d'intégration beaucoup plus élevés. L'utilisation de cette méthode a, par exemple, permis de mettre en évidence que certaines orbites planétaires dans le système solaire sont instables, ce que ne montraient pas des méthodes basées sur l'intégration directe des équations du mouvement.; on a même pu montrer que Mercure pourrait être éjecté du système solaire dans moins de 3.5 milliards d'années lors d'un passage près de Venus ! La méthode de Tree Cette méthode se base sur le fait que les particules interagissent fortement avec ses voisines les plus proches mais beaucoup plus faiblement avec ses voisines les plus lointaines. L'ensemble des forces extérieures agissant sur la particule est donc divisée en forces qui sont dues aux interactions à courte distance et forces dues aux interactions à longue distance. Les forces à courte distance sont calculées de manière rigoureuse sur base de la particule étudiée et de ses voisines immédiates. Les forces à longue distance sont calculées sur base de l'interaction entre la particule étudiée et les particules les plus éloignées regroupées, pour les besoins du calcul, en nuage de particules. On divise l'espace en régions successivement éloignées pour lesquelles l'éloignement plus moins relatif des particules est testée pour savoir si une modélisation en nuage est acceptable ou non. On notera que cette méthode n'exige plus de construire une grille ou un maillage.  Elle permet de modéliser des systèmes entre 10 000 et 1000000 particules. Conclusions On le voit, le problème à n corps est très complexe mais très fécond aussi. Il soulève un commentaire de nature plus générale. Les grandes forces de l'Univers tel qu'on les modélise sont toujours des forces d'interaction à 2 particules. C'est cette manière de modéliser, sur laquelle jusqu'à présent on ne s'est jamais vraiment interrogé (pertinence de cette approche ,…) qui génère une telle complexité déjà à partir du problème à 3 corps. Qui peut en effet affirmer que si on arrivait à un formalisme de description des forces de l'Univers en interaction à 3 corps, tout n'irait pas plus aisément ?   -oOo--

 

   Il y a eu

accès àcette page depuis le 08 mars 2000